1. 그래프란?
그래프(Graph)는 현실세계의 사물이나 개념 간의 연결 관계를 수학적 모델로 단순화 하여 표현한 것이다.
수학정 정의 : 정점 집합 V = {v1, v2, v2, ..., vn} 이고, 정점간의 연결 관계들을 나타내는 간선 집합 E = {(vi, vj)/vi ∈ V, vj ∈ V} ⊆ V x V 일 때, 그래프 G = (V, E) 이다.
2. 그래프 용어
1) 무향 간선 (Undirected Edge)
- 정점을 연결하는 간선에 방향이 존재하지 않는다.
- 임의의 간선 (vi, vj)에 대해서 (vi, vj) = (vj, vi)이다.
2) 유향 간선 (Directed Edge)
- 정점을 연결하는 간선에 방향이 존재한다.
- 임의의 간선 (vi, vj)에 대해서 (vi, vj) ≠ (vj, vi)이다.
3) 인접 (Adjacent)
- 정점 vi, vj에 대해서 간선 e = (vi, vj)가 존재한다. 정점 vi와 vj는 인접한다.
4) 부속 (Incident)
- 정점 vi, vj에 대해서 간선 e = (vi, vj)가 존재한다. 간선 e는 정점 vi와 vj에 부속한다.
5) 차수 (Degree)
- 정점에 부속된 간선의 수
- in-degree : 방향 그래프에서 정점에 들어오는 간선의 수
- out-degree : 방향 그래프에서 정점에서 나가는 간선의 수

6) 다중 간선 (Multiple / Parallel edges)
- c와 d사이에는 다중 간선이 있음
7) self-loop
- a에 연결된 우측 간선은 self-loop
8) 경로 (Path)
- 정점과 간선이 교대로 구성된 sequence
- 단순 경로 (Simple Path) : 정점과 간선이 중복되지 않은 경로
9) 회로 (Cycle)
- 시작 정점과 끝 정점이 같은 경로
- 단순 회로 (Simple Cycle) : 정점과 간선이 중복되지 않은 회로
10) 연결됨 (Connected)
- 정점 vi에서 정점 vj로의 경로가 존재하면, 정점 vi와 정점 vj는 연결되어 있다고 한다.
3. 그래프 종류
1) 무향 그래프 (Undirected Graph)

- 무향 간선으로 이루어진 그래프
2) 유향 그래프 (Directed Graph)

- 유향 간선으로 이루어진 그래프
3) 가중치 그래프 (Weighted Graph)

- 가중치(혹은 비용)를 갖는 간선으로 이루어진 그래프
4) 정규 그래프 (Regular Graph)
- 모든 정점이 동일한 차수를 가지는 그래프
5) 완전 그래프 (Complete Graph)
- 임의의 두 정점 vi, vj에 대해서 vi, vj를 잇는 간선 Edge(vi, vj)이 존재하는 그래프
- 완전 그래프는 정규 그래프이다.
- N개의 정점을 가지는 무향 그래프의 경우 간선의 개수 = 1/2 * N(N-1)
- N개의 정점을 가지는 유향 그래프의 경우 간선의 개수 = N(N-1)
6) 연결 그래프 (Connected Graph
- 임의의 두 정점 vi, vj에 대해서 경로 Path(vi, vj)가 존재하는 그래프
7) 부분 그래프
- 어떤 그래프의 정점집합의 부분집합과 그에 속한 간선들로 이루어진 그래프
- 어떤 그래프의 간선집합의 부분집합과 그에 속한 정점들로 이루어진 그래프
8) 트리 그래프
- 순환을 갖지 않는 연결 그래프
- 임의의 두 정점에 대해서 경로가 정확히 1개 존재한다.
- 하나 이상의 정점을 가지며, 임의의 간선 e를 제거한 그래프는 연결 그래프가 아니다.
3. 그래프 표현
1) 간선 리스트 (Edge List)

- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 E*2 (or E*3) 이차원 배열 A에 간선 정보 저장
- 어떤 두 정점 vi, vj를 연결하는 간선 ek=(vi, vj)에 대해서 A[k][0]= vi, A[k][1]=vj
- 가중치 그래프의 경우 배열의 3번째 열에 간선의 가중치 저장
- 이는 정점의 수에 비해 간선의 수가 매우 작을 때 사용하기도 한다.
2) 인접 행렬 (Adjacency Matrix)
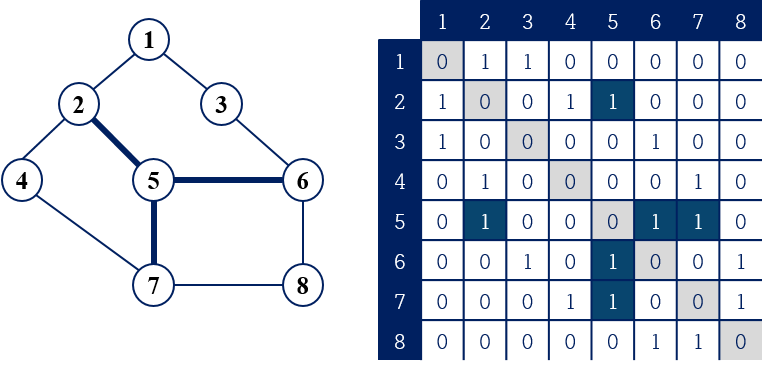

- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V*V 이차원 배열 A에 그래프 정보 저장
- 어떤 정점 vi, vj를 연결하는 간선 ek=(vi, vj)가
존재하면 => A[i][j] = 1(or 가중치)
존재하지 않으면 => A[i][j] = 0
- 어떤 정점 vi, vj가
인접하면 => A[i][j] = 1(or 가중치)
인접하지 않으면 => A[i][j] = 0
3) 인접 리스트 (Adjacent List)

- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V개의 연결 리스트로 그래프 정보를 저장
- 일반적으로 List(or Vector)의 배열로 구현
4. 그래프 표현 방식 비교
| V개의 정점 E개의 간선 중복간선 없음 self-loops 없음 |
간선 리스트 | 인접 행렬 | 인접 리스트 |
| 공간 | E | V^2 | V + E |
| 정점 VA의 부속 간선 | E | V | deg(VA) (차수) |
| 정점 VA, VB 인접 여부 | E | 1 | min(deg(VA), deg(VB)) |
| 정점 삽입 | 1 | V^2 | 1 |
| 간선 삽입 | 1 | 1 | 1 |
참고 사이트
'BASE > Structure' 카테고리의 다른 글
| 자료구조 - 비순환 방향 그래프 (DAG, Directed Acyclic Graph) (0) | 2021.02.02 |
|---|---|
| 자료구조 - 서로소 집합 (0) | 2021.02.02 |
| 자료구조 - 맵 (Map) (0) | 2021.01.27 |
| 자료구조 - 세트 (Set) (0) | 2021.01.27 |
| 자료구조 - 트라이 (Trie) (0) | 2021.01.27 |


댓글