알고리즘 - 최단 경로 알고리즘 (다익스트라 알고리즘, 벨만-포드 알고리즘, 플로이드-워셜 알고리즘)
1. 최단 경로 알고리즘
최단 경로 문제란 가중 그래프에서 간선의 가중치의 합이 최소가 되는 경로를 찾는 문제이다.
1) 최단 경로 문제의 종류
- 단일 출발 (single-source) 최단 경로
- 어떤 하나의 정점에서 출발하여 나머지 모든 정점 까지의 최단 경로를 찾는 문제
- 단일 도착 (single-destination) 최단 경로
- 모든 정점에서 출발하여 어떤 하나의 정점까지의 최단 경로를 찾는 문제로 그래프 내의 간선들을 뒤집으면 단일 출발 최단거리 문제로 바뀔 수 있다.
- 단일 쌍(single-pair) 최단 경로
- 모든 정점 쌍들 사이의 최단 경로를 찾는 문제
2) 주요 알고리즘
- BFS (완전탐색 알고리즘)
- 가중치가 없거나 모든 가중치가 동일한 그래프에서 최단경로를 구하는 경우 가장 빠르다
- 다익스트라 알고리즘 (Dijkstra Algorithm)
- 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm)
- 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
- 전체 쌍 최단 경로 문제
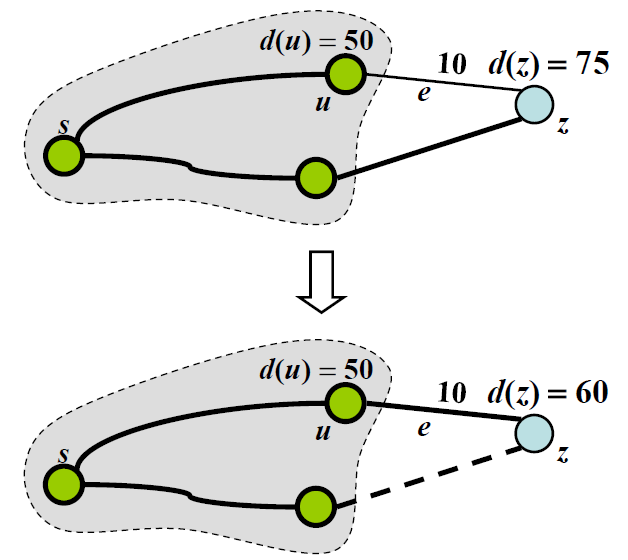
2. 다익스트라 알고리즘 (Dijkstra Algorithm)


1) 다익스트라 알고리즘이란?
V개의 정점과 음수가 아닌 E개의 간선을 가진 그래프 G에서 특정 출발 정점(S)에서 부터 다른 모든 정점까지의 최단경로를 구하는 알고리즘
D[S]=0 (출발점을 0으로 저장)
방문하지 않은 정점 중에서 D[K]가 최소인 정점 I 선택
D[J] = D[I] + W 로 갱신
특징
- 각 정점을 최대 한 번씩만 방문하여 최단 거리를 확정한다. (음의 가중치를 가질 수 없다.)
- 아직 방문하지 않은 정점들 중 최단거리인 점을 찾아 방문하여 최단거리를 확정하고, 이를 반복하는 방식으로 진행된다.
- 총 V*V번 연산이 필요하다. 따라서 O(V^2)의 시간복잡도를 가진다.
- 방문하지 않은 정점 중에서 최단 거리가 최소인 정점을 찾는 과정에서 우선순위 큐 혹은 힙 자료구조를 이용하면 더욱 개선된 알고리즘이 가능하다.
2) 개선된 알고리즘 단계
D[S]=0 (출발점을 0으로 저장) + 최소 힙에 출발점 S 삽입
최소 힙에서 맨 위에 있는 정점 I 꺼냄
D[J] = D[I] + W 로 갱신 + 최소 힙에 정점 J 삽입
특징
- 최악의 경우 모든 간선을 확인할 때 마다 거리 배열이 갱신이 된다고 하면, 최소 힙에는 최대 E번 정점을 넣게 된다. (간선의 개수가 E개 이기 때문)
- 최소 힙에 E개의 정점이 있을 때, 하나의 정점을 꺼낼 때 마다 logE의 연산이 필요하다. (최소 힙 삭제연산의 시간복잡도)
- ElogE = ElogV^2 = 2ElogV
- 즉, 최소 힙 혹은 우선순위 큐를 사용하는 경우, 시간 복잡도는 O(ElogV)이다.
3. 벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm)


V개의 정점과 E개의 간선을 가진 가중 그래프 G에서 특정 출발 정점(S)에서 부터 다른 모든 정점까지의 최단경로를 구하는 알고리즘이다.
V개의 정점과 E개의 간선을 가진 가중 그래프에서 어떤 정점 A에서 어떤 정점 B까지의 최단거리는 최대 V-1개의 간선을 사용한다. (시작 정점 A를 포함하여 최대 V개의 정점을 지난다.)
특징
- 음의 가중치를 가지는 간선도 가능하다.
- 음의 사이클의 존재 여부를 확인할 수 있다.
- 최단거리를 구하기 위해서 V-1번 E개의 모든 간선을 확인한다.
- 음의 사이클 존재 여부를 확인하기 위해서 한 번 더 E개의 간선을 확인한다.
- 총 연산횟수는 V*E이다. 따라서 시간복잡도는 O(VE)이다.
- V번째 모든 간선을 확인하였을 때 거리 배열이 갱신되었다면, 그래프 G는 음의 사이클을 가지는 그래프이다.
- 그래프 모든 엣지에 대해 edge relaxation을 시작노드를 제외한 전체 노드수 만큼 반복 수행한 뒤, 마지막으로 그래프 모든 엣지에 대해 edge relaxation을 1번 수행해 준다. 이때 한번이라도 업데이트가 일어난다면 음의 사이클이 존재한다는 뜻이 되어서 결과를 구할 수 없다는 의미의 false를 반환하고 함수를 종료한다.
4. 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)


V개의 정점과 E개의 간선을 가진 가중 그래프 G에서 모든 정점 사이의 최단 경로를 구하는 알고리즘이다.
어떤 두 정점 사이의 최단 경로는 어떤 경유지(K)를 거치거나 거치지 않는 경로 중 하나이다. 즉, 정점 A와 정점 B 사이의 최단 경로는 A-B이거나 A-K-B이다. 만약 경유지(K)를 거친다면 최단 경로를 이루는 부분 경로 역시 최단 경로이다. 다시 말해, 만약 A-B의 최단 경로가 A-K-B라면 A-K와 K-B도 각각 최단 경로이다.
특징
- 순환만 없다면 음수 가중치도 가능하다.
- 기본적으로 동적계획법으로 접근한다. 모든 가능한 경유지에 대해서 모든 정점에서 모든 정점으로 가는 최단거리를 확인하므로 연산횟수는 V^3이고, 따라서 시간복잡도는 O(V^3)이다.
- 구현이 쉽고 모든 지점에서 최단 경로를 구하는 것이 가능하다.
'BASE > Alogorithm' 카테고리의 다른 글
| 알고리즘 - 단절점 (Articulation Points / Cut Vertices) (0) | 2021.02.03 |
|---|---|
| 알고리즘 - 최소 공통 조상 (LCA, Lowest Common Ancestor) (0) | 2021.02.03 |
| 알고리즘 - 크루스칼 알고리즘(Kruskal's Algorithm), 프림 알고리즘(Prim's Algorithm) (0) | 2021.02.02 |
| 알고리즘 - 위상정렬 (Topological Sort) (0) | 2021.02.02 |
| 알고리즘 - 에라토스네스의 체 (0) | 2021.02.02 |




댓글